A mixture prior

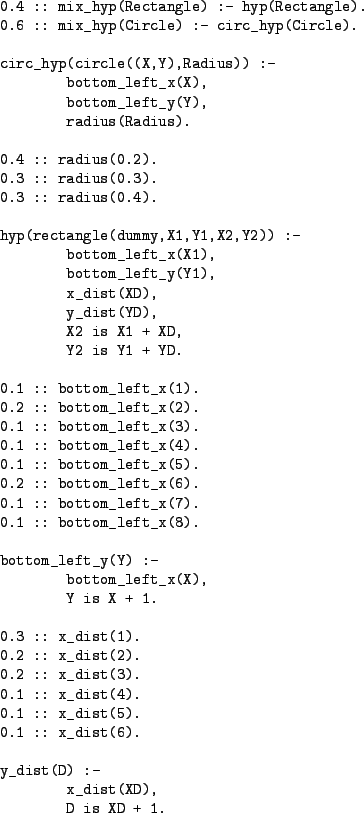
Because of the nature of the prior distributions defined by SLPs, it is very easy to formulate mixture priors. Fig 16 contains our original hyp/1 prior over rectangles, a new circ_hyp/1 prior over circles and a mixture prior mix_hyp/1 which mixes the hyp/1 and circ_hyp/1 priors to give a distribution over rectangles and circles. The likelihood function must now be extended to compute the likelihood of circles: see Fig 17 to see how this is done. Since the mixture prior has a bias towards circles, circles are visited more frequently when MCMCMS is run.

Figure 16: Mixture prior over rectangles and circles (found in the file tutorial/slps/mixture.slp).

Figure 17: The file tutorial/mixture_concept_learning.pl which includes additional clauses to compute `noisy' likelihoods for circle hypotheses