Tempering

A number of hot chains that are developed in parallel to the main cold chain can be run. Hot chains move on smoother likelihood spaces, so getting less stuck. At each iteration two chains are chosen for a possible swap of their, next-iteration, current models.

Power tempering is the only kind of tempering supported. In the future other kinds might be possible. In power tempering the space is smoothed by raising the likelihood to a power. For hot chain $j$ we sample from stationary distribution $\ensuremath{\pi}_{\beta_{j}}(x) \propto \ensuremath{\pi_{0}}(x)L(x)^{\beta_{j}}$ for $0 < \beta_{j} < 1$. Proposals and acceptances within this chain work exactly as for the cold chain. The only difference is that there is a different likelihood. So, if at model $\ensuremath{{M_i^j}}$ we propose model $\ensuremath{{M_*^j}}$ then:

$$\alpha_{j}(\ensuremath{{M_i^j}} ,\ensuremath{{M_*^j}} ) = \... ...*^j}} )}{L(\ensuremath{{M_i^j}} )}\right)^{\beta_{j}} \right\}$$

where $\kappa(\ensuremath{{M_i^j}} ,\ensuremath{{M_*^j}} )$ is the combined prior and proposal conttribution.

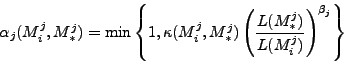
The chain-swap acceptance probability for moves between chains does not depend on the proposal distribution which generates moves within chains. So the acceptance probability is the same for all within-chain proposals, namely:

$$\alpha(\ensuremath{{M_\alpha^{j_1}}} ,\ensuremath{{M_\alpha^... ...{M_\alpha^{j_1}}} )}\right]^{(\beta_{1} - \beta_{2})} \right\}$$

where $\ensuremath{{M_\alpha^{j_1}}}$ is the accepted within-chain model in chain $j_1$.

An example run-script using power tempering can be found in carts/pima/run_hot.pl.